TIME AND THE MOVING CLOCK :
Time never seems to do what we want it to. There never seems to be enough of it when we're late for work or school, but far too much of it when we have to stand in the pouring rain waiting for a bus. These annoyances apart, it seems that time flows along smoothly; never bending, never changing its rate: always "on time". This steady flow is so reliable that we fit our lives around it. We start the day when the clock tells us to, work when it tells us to, eat when it tells us to, and go to bed when it tells us to. Time, it seems, is constant.
This equation seems to solve the problem. We can now predict the energy of a moving body and take into account the mass increase. What's more, we can rearrange the equation to show that:
Time never seems to do what we want it to. There never seems to be enough of it when we're late for work or school, but far too much of it when we have to stand in the pouring rain waiting for a bus. These annoyances apart, it seems that time flows along smoothly; never bending, never changing its rate: always "on time". This steady flow is so reliable that we fit our lives around it. We start the day when the clock tells us to, work when it tells us to, eat when it tells us to, and go to bed when it tells us to. Time, it seems, is constant.
That the flow of time is constant is seemingly obvious and this has been the prevailing view for almost all of human history. Sir Isaac Newton, when he wasn't dodging falling apples, certainly thought time was constant. He gave us the idea of a "clockwork universe", in which it would be possible to know not only all of the past but all of the future if only we could say where every particle was, in what direction each particle was moving and at what speed. This model assumed, not unreasonably, that time flows at an ever constant rate. As brilliant as Newton was, he was, much to everyone's surprise, wrong.
In 1905 Albert Einstein published his Special Theory of Relativity. This work considered time not as a single constantly flowing entity, but as part of a much more complex system, linked with that of space itself. This is called space-time. Because space and time are part of the same entity it's impossible to move in space without moving in time. Time, for anything moving, changes.
One of the most startling consequences of special relativity is that any moving clock slows down relative to a stationary observer. There are of course many different types of clock, such as digital watches, clockwork clocks, atomic clocks and even our own biological clocks but they are all equally affected by the same principle, namely: MOVING CLOCK RUN SLOW.
Spacetime Diagrams :
The spacetime diagram is a useful visualisation technique.
The time axis is vertical, and of course we have multiplied t by c so we are measuring time in meters, the same as the other coordinates.
An object that is stationary does not have its position change with time: on a spacetime diagram this would be represented by a worldline that is vertical.
If an object is moving, its worldline is not vertical.
For something moving at the speed of light, it moves a distance of, say, 1 meter in a time of 1 meter. Thus the worldline makes an angle of 45 degrees with both the x and ct axes. In the diagram, we have drawn the light cone, representing rays of light that go through the point x=0 and ct=0.
The point x=0 and ct=0 is called the present. Coordinates in spacetime that are inside the light cone and have time coordinates greater than zero are in the future; locations inside the light cone with negative time are in the past.
Consider that we are located at the present. We know that, for example, we can not know what happened at the star Alpha Centauri yesterday; it is about 4 light years away and since no information can travel faster than the speed of light we will have to wait four years to find out what happened there. Thus the coordinate of Alpha Centauri yesterday, which is outside the light cone, is inaccessible to us. Similarly, we can not get a signal to Alpha Centauri that will arrive tomorrow. Thus the entire region of spacetime outside the light cone is called elsewhere.
WHY TIME RUN SLOW IN SPEED :
We are going far too slowly for any noticeable change to take place.Even if we go at high enough speeds to bring about a large slowing down of local time we wouldn't notice because our own body clocks would also be running just as slowly.
The speed of light is very close to 300,000 km per second (186,300 miles per second). It isn't until we get to speeds that are a large fraction of the speed of light that any change in the flow of time becomes apparent. However, at speeds very close to that of light the effect grows in magnitude very rapidly indeed until time almost comes to a standstill.This slowing down of clocks due to high speeds is called time dilation and has a precise mathematical relationship. For the sake of completeness I have included the relevant equation below but you can skip over it and move on to the graph below it if you prefer. The equation for time dilation is:
So, when we move, at whatever speed, time slows down relative to a stationary observer. But note that, for example, the occupants of a rocket travelling at very high speeds would still experience time passing normally. However, if they could see out to an Earth-bound clock it would appear, to them, to be running too quickly. If an Earth-bound observer could see a clock inside the rocket it would appear to be running too slowly. This is why the theory is called "relativity", it is because time is relative to whoever is observing it at a particular speed.
MASS INCREASED DUE TO VELOCITY :
As our speed goes ever higher so the apparent mass increases, and so does the energy required to move it. At the speed of light it would take infinite energy to move any mass. Since it's clearly impossible to obtain infinite energy we can never quite reach the speed of light (but we can get as close as our energy supply, and technology, will allow). Note that the occupants of any rocket travelling at very high speeds will not be aware of any increase in mass, just as they wouldn't be aware in any change in the rate that time passes. It's only when they measure the mass of stationary observers that they will see that there has been a change in mass -- the astronauts will perceive that everything around them and their rocket has changed its mass while their own seems to have remained constant
Relativistic Mass Formula
Relativistic mass refers to mass of a body which change with the speed of the body as this speeds approaches close to speed of light, it increases with velocity and tends to infinity when the velocity approaches the speed of light.
Relativistic mass = rest mass / squared root [one minus (velocity / speed of light) squared]
The equation is:
mr = m0 / sqrt (1 – v2 / c2 )
Where:
mr: relativistic mass
m0: rest mass (invariant mass)
v: velocity
c: speed of light
THE EQUATION :
In order to compensate for the apparent mass increase due to very high speeds we have to build it into our equations. We know that the mass increase can be accounted for by using the equation:
From this equation we know that mass (m) and the speed of light (c) are related in some way. What happens if we set the speed (v) to be very low? Einstein realized that if this is done we can account for the mass increase by using the term mc2 (the exact arguments and mathematics required to derive this are quite advanced, but an example is provided here). Using this term we now have an equation that takes into account both the kinetic energy and the mass increase due to motion, at least for low speeds
This equation seems to solve the problem. We can now predict the energy of a moving body and take into account the mass increase. What's more, we can rearrange the equation to show that:
This result is fine for low speeds, but what about speeds closer to the speed of light? We know that mass increases at high speeds, but according to the Newtonian part of the equation that isn't the case. Therefore, we need to replace the Newtonian part of the formula in order to make the equation correct at all speeds. How can we do this?We know that E – mc2 is approximately equal to the Newtonian kinetic energy when v is small, so we can use E – mc2 as the definition of relativistic kinetic energy:
We have now removed the Newtonian part of the equation. Note that we haven’t given a formula for relativistic kinetic energy. The reason for this will become apparent in a moment. Rearranging the result shows that:
It can now be seen that relativistic energy consists of two parts. The first part is kinetic and depends on the speed of the moving body, while the second part is due to the mass increase and does not depend on the speed of the body. However, both parts must be a form of energy, but what form? We can simplify the equation by setting the speed (i.e. the relativistic kinetic energy) of the moving body to be zero, thereby removing it from the equation:
We now have the famous equation in the form it's most often seen in, but what does it mean?We have seen that a moving body apparently increases in mass and has energy by virtue of its speed (the kinetic energy). Looking at the problem another way we can say that as the speed of a body gets lower there will be less and less kinetic energy until at rest the body will have no kinetic energy at all. So far so good, but what about the mass due to the speed of the body? Again, as the body slows down the mass will become progressively smaller but it can't reach zero. As noted near the start of the page, the lowest the mass can be is unity (1) and we can't just make the body disappear into nothing. The lowest possible mass the body can have is its "rest mass", i.e. the mass the body has when it is at rest. But the equation we have derived (E = mc2) isn't for mass, it's for energy. The energy must somehow be locked up in the mass of the body
:
:







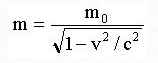


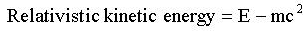

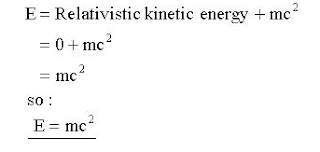




No comments:
Post a Comment