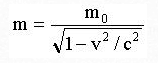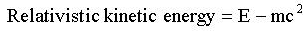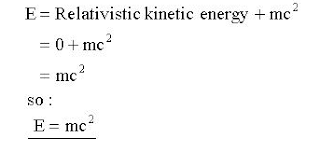QUANTUM LOGIC GATE

Quantum Logic Gates :

Traditional computers are like microscopic cities. The roads of these cities are wires with electricity coursing through them. These roads have lots of gates, known as logic gates, which enable computers to do their job. Like physical gates that allow or block cars, logic gates allow or block electricity. Electricity that goes through the gates represents a “1” of digital data, and blocked electricity is a “0.”

Logic gates are building blocks for processing information. One kind of logic gate, known as the AND gate, could, for example, quickly determine whether two people agree to a business deal. It takes in two bits of information, and generates a 1 if both incoming bits are 1 s. So, if both business people say “yes” (1) to the deal, the AND gate will output 1. If one or both say “no” (0), the AND gate generates a 0 or a no.

By arranging gates in a circuit, engineers can create something akin to a flowchart that enables computers to carry out many kinds of logical operations, such as mathematical calculations and perform the kinds of tasks that computers can do.

In their quantum logic gate, BY controlle the energy levels in an individual ion so that a lower-energy state represented a 0 and a higher-energy state represented a 1. The ion’s internal energy was the first q bit. They created a second quantum bit with the atom’s external motion: 0 represented less motion and 1 represented a greater amount of motion.

The group entangled the ion’s internal energy state with its overall motion. In the process, they made a quantum version of a CONTROLLED NOT gate. In their gate, the ion’s energy of motion serves the “control” bit. If it is a 1, then it causes the ion’s internal energy state to flip.

Quantum gates are usually represented as matrices. A gate which acts on k qubits is represented by a 2^k x 2^k unitary matrix. The number of qubits in the input and output of the gate have to be equal. The action of the gate on a specific quantum state is found by multiplying the vector which represents the state by the matrix representing the gate. In the following, the vector representation of a single qubit is:

Hadamard (H) gate

The Hadamard gate acts on a single qubit. It maps the basis state  to  and  to , which means that a measurement will have equal probabilities to become 1 or 0 . It represents a rotation of  about the axis .s. It is represented by the Hadamard matrix.

${\displaystyle H={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}}$The hadamard gate is the one-qubit version of the quantum furier trasform..

Since ${\displaystyle HH^{*}=I}$ where I is the identity matrix, H is indeed a unity matrix.

Pauli-X gate

The Pauli-X gate acts on a single qubit. It is the quantum equivalent of the NOT gate for classical computers (with respect to the standard basis , 

 which privileges the Z-direction) . It equates to a rotation of the bloch spare around the X-axis by pai radians. I Due to this nature, it is sometimes called bit flip.It is represented by the pauli metrix

Pauli-Y gate

The Pauli-Y gate acts on a single qubit. It equates to a rotation around the Y-axis of the Bloch sphere by pai radians. 

${\displaystyle Y={\begin{bmatrix}0&-i\\i&0\end{bmatrix}}}$.

Pauli-Z gate

The Pauli-Z gate acts on a single qubit. It equates to a rotation around the Z-axis of the Bloch sphere by ${\displaystyle \pi }$ radians. Thus, it is a special case of a phase shift gate (which are described in a next subsection) with ${\displaystyle \phi =\pi }$. It leaves the basis state ${\displaystyle |0\rangle }$ unchanged and maps ${\displaystyle |1\rangle }$ to ${\displaystyle -|1\rangle }$. Due to this nature, it is sometimes called phase-flip. It is represented by the pauli Z matrix:

${\displaystyle Z={\begin{bmatrix}1&0\\0&-1\end{bmatrix}}}$.

Square root of NOT gate (√NOT)

The NOT gate acts on a single qubit. so this gate is a square root of the NOT gate.

Similar squared root-gates can be constructed for all other gates by finding the unitary matrix that, multiplied by itself, yields the gate one wishes to construct the squared root gate of. All rational exponents of all gates can be created in this way. (Only approximations of irrational exponents are possible to synthesize from composite gates whose elements are not themselves irrational, since exact synthesis would result in infinite gate depth.)

Phase shift (${\displaystyle R_{\phi }}$) gates

This is a family of single-qubit gates that leave the basis state  unchanged and map  to  The probability of measuring a  or  is unchanged after applying this gate, however it modifies the phase of the quantum state. This is equivalent to tracing a horizontal circle (a line of latitude) on the Bloch sphere by ${\displaystyle \phi }$ radians.

{\displaystyle R_{\phi }={\begin{bmatrix}1&0\\0&e^{i\phi }\end{bmatrix}}}

where the phase shift. Some common examples are the  gate (commonly written as T) where , the phase gate (written S, though S is sometimes used for SWAP gates) where and the Pauli-Z gate where.

Swap (SWAP) gate

.

The swap gate swaps two qubits.

 With respect to the basis, it is represented by the matrix:

Square root of Swap gate (√SWAP)

The sqrt(swap) gate performs half-way of a two-qubit swap. It is universal such that any quantum many qubit gate can be constructed from only sqrt(swap) and single qubit gates. 

The sqrt(swap) gate is not, however maximally entangling, more than one application of it is required to produce a Bell state from product states.

Controlled (cX cY cZ) gates

Controlled gates act on 2 or more qubits, where one or more qubits act as a control for some operation. For example, the controlled NOT gate (or CNOT or cX) acts on 2 qubits, and performs the NOT operation on the second qubit only when the first qubit is , and otherwise leaves it unchanged. With respect to the basis, it is represented by the matrix:

More generally if U is a gate that operates on single qubits with matrix representation

then the controlled-U gate is a gate that operates on two qubits in such a way that the first qubit serves as a control. It maps the basis states as follows.

${\displaystyle |00\rangle \mapsto |00\rangle }$The matrix representing the controlled U is

The CNOT gate is generally used in quantum computing to generate entangled states.When U is one of the pauli matrices, σ_x, σ_y, or σ_z, the respective terms "controlled-X", "controlled-Y", or "controlled-Z" are sometimes used.

Toffoli (CCNOT) gate

The Toffoli gate, also CCNOT gate or Deutsch ${\displaystyle D(\pi /2)}$ gate, is a 3-bit gate, which is universal for classical computation. The quantum Toffoli gate is the same gate, defined for 3 qubits. If the first two bits are in the state, it applies a Pauli-X (or NOT) on the third bit, else it does nothing. It is an example of a controlled gate. Since it is the quantum analog of a classical gate, it is completely specified by its truth table. The Toffoli gate is universal when combined with the single qubit Hadamard gate.

Fredkin (CSWAP) gate

The Fredkin gate (also CSWAP or cS gate) is a 3-bit gate that performs a controlled swap. It is universal for classical computation. It has the useful property that the numbers of 0s and 1s are conserved throughout, which in the billiard ball model means the same number of balls are output as input.

Ising (XX) gate

The Ising gate (or XX gate) is a 2-qubit gate that is implemented natively in some trapped-ion quantum computers. It is defined as

{\displaystyle XX_{\phi }={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1&0&0&-ie^{i\phi }\\0&1&-i&0\\0&-i&1&0\\-ie^{-i\phi }&0&0&1\\\end{bmatrix}}={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1&0&0&e^{i(\phi -\pi /2)}\\0&1&-i&0\\0&-i&1&0\\e^{i(-\phi -\pi /2)}&0&0&1\\\end{bmatrix}}}

Deutsch gate

Deutsch  gate is a three-qubit gate. It is defined as

{\displaystyle |a,b,c\rangle \mapsto {\begin{cases}i\cos(\theta )|a,b,c\rangle +\sin(\theta )|a,b,1-c\rangle &{\mbox{for }}a=b=1\\|a,b,c\rangle &{\mbox{otherwise.}}\end{cases}}}

Unfortunately, a working Deutsch gate has remained out of reach, due to lack of a protocol. However, a method was proposed to realize such  with dipole-dipole interaction in neutral atoms.

DIGITAL LOGIC GATES

Digital Logic | Logic Gates :

In Boolean Algebra, there are three basic operations,  which are analogous to dis-junction, conjunction, and negation in propositional logic. Each of these operations has a corresponding logic gate. Apart from these there are a few other logic gates as well.
Digital logic gates may have more than one input, (A, B, C, etc.) but generally only have one digital output, (Q). Individual logic gates can be connected together to form combinational or sequential circuits, or larger logic gate functions.
Integrated Circuits or IC’s as they are more commonly called, can be grouped together into families according to the number of transistors or “gates” that they contain. For example, a simple AND gate my contain only a few individual transistors, were as a more complex microprocessor may contain many thousands of individual transistor gates. Integrated circuits are categorised according to the number of logic gates or the complexity of the circuits within a single chip with the general classification for the number of individual gates given as:

Logic Gates –

• AND gate(.) – The AND gate gives an output of 1 if both the two inputs are 1, it gives 0 otherwise.
• OR gate(+) – The OR gate gives an output of 1 if either of the two inputs are 1, it gives 0 otherwise.

NOT gate(‘) – The NOT gate gives an output of 1 input is 0 and vice-versa.

• XOR gate(⊕) – The XOR gate gives an output of 1 if either both inputs are different, it gives 0 if they are same.

Three more logic gates are obtained if the output of above-mentioned gates is negated.

• NAND gate(↑)- The NAND gate (negated AND) gives an output of 1 if both inputs are 0, it gives 1 otherwise.
• NOR gate(↓)- The NOR gate (negated OR) gives an output of 1 if both inputs are 0, it gives 1 otherwise.

XNOR gate(⊙)- The XNOR gate (negated XOR) gives an output of 1 both inputs are same and 0 if both are different.

Boolean Algebra :

Boolean Algebra is used to analyze and simplify the digital (logic) circuits. It uses only the binary numbers i.e. 0 and 1. It is also called as Binary Algebra or logical Algebra

Following are the important rules used in Boolean algebra.

1.   Variable used can have only two values. Binary 1 for HIGH and Binary 0 for LOW.2.   Complement of a variable is represented by an overbar (-).

3.  ORing of the variables is represented by a plus (+) sign between them. For example ORing of A, B, C is represented as A + B + C.

4.  Logical ANDing of the two or more variable is represented by writing a dot between them such as A.B.C. Sometime the dot may be omitted like ABC.

Digital Logic States :

The Digital Logic Gate is the basic building block from which all digital electronic circuits and microprocessor based systems are constructed from. Basic digital logic gates perform logical operations of AND, OR and NOT on binary numbers.

In digital logic design only two voltage levels or states are allowed and these states are generally referred to as Logic “1” and Logic “0”, High and Low, or True and False. These two states are represented in Boolean Algebra and standard truth tables by the binary digits of “1” and “0” respectively

Most digital logic gates and digital logic systems use “Positive logic”, in which a logic level “0” or “LOW” is represented by a zero voltage, 0v or ground and a logic level “1” or “HIGH” is represented by a higher voltage such as +5 volts, with the switching from one voltage level to the other, from either a logic level “0” to a “1” or a “1” to a “0” being made as quickly as possible to prevent any faulty operation of the logic circuit.

Every Logic gate has a graphical representation or symbol associated with it. Below is an image which shows the graphical symbols and truth tables associated with each logic gate.

Logic AND Gate :

A Logic AND Gate is a type of digital logic gate whose output goes HIGH to a logic level 1 when all of its inputs are HIGH.

The output state of a “Logic AND Gate” only returns “LOW” again when ANY of its inputs are at a logic level “0”. In other words for a logic AND gate, any LOW input will give a LOW output.

The logic or Boolean expression given for a digital logic AND gate is that for Logical Multiplication which is denoted by a single dot or full stop symbol, ( . ) giving us the Boolean expression of:  A.B = Q.

Logic OR Gate :

A Logic OR Gate is a type of digital logic gate whose output goes HIGH to a logic level 1 when one or more of its inputs are HIGH.

The output, Q of a “Logic OR Gate” only returns “LOW” again when ALL of its inputs are at a logic level “0”. In other words for a logic OR gate, any “HIGH” input will give a “HIGH”, logic level “1” output.

The logic or Boolean expression given for a digital logic OR gate is that for Logical Addition which is denoted by a plus sign, ( + ) giving us the Boolean expression of:  A+B = Q.

Exclusive-OR Gate :

The Exclusive-OR logic function is a very useful circuit that can be used in many different types of computational circuits.

In the previous tutorials, we saw that by using the three principal gates, AND Gate, the OR Gate and the NOT Gate, we can build many other types of logic gate functions, such as a NAND Gate and a NOR Gate or any other type of digital logic function we can imagine.

But there are two other types of digital logic gates which although they are not a basic gate in their own right as they are constructed by combining together other logic gates, their output Boolean function is important enough to be considered as complete logic gates. These two “hybrid” logic gates are called the Exclusive-OR (Ex-OR) Gate and its complement the Exclusive-NOR (Ex-NOR) Gate.

Previously, we saw that for a 2-input OR gate, if A = “1”, OR B = “1”, OR BOTH A + B = “1” then the output from the digital gate must also be at a logic level “1” and because of this, this type of logic gate is known as an Inclusive-OR function. The gate gets its name from the fact that it includes the case of Q = “1” when both A and B = “1”.

If however, an logic output “1” is obtained when ONLY A = “1” or when ONLY B = “1” but NOT both together at the same time, giving the binary inputs of “01” or “10”, then the output will be “1”. This type of gate is known as an Exclusive-OR function or more commonly an Ex-Or function for short. This is because its boolean expression excludes the “OR BOTH” case of Q = “1” when both A and B = “1”.

In other words the output of an Exclusive-OR gate ONLY goes “HIGH” when its two input terminals are at “DIFFERENT” logic levels with respect to each other.

An odd number of logic “1’s” on its inputs gives a logic “1” at the output. These two inputs can be at logic level “1” or at logic level “0” giving us the Boolean expression of:  Q = (A ⊕ B) = A.B + A.B

The Exclusive-OR Gate function, or Ex-OR for short, is achieved by combining standard logic gates together to form more complex gate functions that are used extensively in building arithmetic logic circuits, computational logic comparators and error detection circuits.

Logic NAND GATE :

The Logic NAND Gate is a combination of a digital logic AND gate and a NOT gate connected together in series.

The logic or Boolean expression given for a logic NAND gate is that for Logical Addition, which is the opposite to the AND gate, and which it performs on the complements of the inputs. The Boolean expression for a logic NAND gate is denoted by a single dot or full stop symbol, ( . ) with a line or Overline, ( ‾‾ ) over the expression to signify the NOT or logical negation of the NAND gate giving us the Boolean expression of:  A.B = Q.

Logic NOR Gate :

The Logic NOR Gate gate is a combination of the digital logic OR gate and an inverter or NOT gate connected together in series

The logic or Boolean expression given for a logic NOR gate is that for Logical Multiplicationwhich it performs on the complements of the inputs. The Boolean expression for a logic NOR gate is denoted by a plus sign, ( + ) with a line or Overline, ( ‾‾ ) over the expression to signify the NOT or logical negation of the NOR gate giving us the Boolean expression of:  A+B = Q.

Exclusive-NOR Gate :

The Exclusive-NOR Gate function is a digital logic gate that is the reverse or complementary form of the Exclusive-OR function.

Basically the “Exclusive-NOR Gate” is a combination of the Exclusive-OR gate and the NOT gate but has a truth table similar to the standard NOR gate in that it has an output that is normally at logic level “1” and goes “LOW” to logic level “0” when ANY of its inputs are at logic level “1”.

However, an output “1” is only obtained if BOTH of its inputs are at the same logic level, either binary “1” or “0”. For example, “00” or “11”. This input combination would then give us the Boolean expression of:  Q = (A ⊕ B) = A.B + A.B

ALBERT EINSTEIN's Time Dilation - E = mc2 Explained

TIME AND THE MOVING CLOCK :

Time never seems to do what we want it to. There never seems to be enough of it when we're late for work or school, but far too much of it when we have to stand in the pouring rain waiting for a bus. These annoyances apart, it seems that time flows along smoothly; never bending, never changing its rate: always "on time". This steady flow is so reliable that we fit our lives around it. We start the day when the clock tells us to, work when it tells us to, eat when it tells us to, and go to bed when it tells us to. Time, it seems, is constant.

That the flow of time is constant is seemingly obvious and this has been the prevailing view for almost all of human history. Sir Isaac Newton, when he wasn't dodging falling apples, certainly thought time was constant. He gave us the idea of a "clockwork universe", in which it would be possible to know not only all of the past but all of the future if only we could say where every particle was, in what direction each particle was moving and at what speed. This model assumed, not unreasonably, that time flows at an ever constant rate. As brilliant as Newton was, he was, much to everyone's surprise, wrong.

                                                                 

In 1905 Albert Einstein published his Special Theory of Relativity. This work considered time not as a single constantly flowing entity, but as part of a much more complex system, linked with that of space itself. This is called space-time. Because space and time are part of the same entity it's impossible to move in space without moving in time. Time, for anything moving, changes.

One of the most startling consequences of special relativity is that any moving clock slows down relative to a stationary observer. There are of course many different types of clock, such as digital watches, clockwork clocks, atomic clocks and even our own biological clocks but they are all equally affected by the same principle, namely: MOVING CLOCK RUN SLOW.

Spacetime Diagrams :

The spacetime diagram is a useful visualisation technique.

The time axis is vertical, and of course we have multiplied t by c so we are measuring time in meters, the same as the other coordinates.

An object that is stationary does not have its position change with time: on a spacetime diagram this would be represented by a worldline that is vertical.

If an object is moving, its worldline is not vertical.

For something moving at the speed of light, it moves a distance of, say, 1 meter in a time of 1 meter. Thus the worldline makes an angle of 45 degrees with both the x and ct axes. In the diagram, we have drawn the light cone, representing rays of light that go through the point x=0 and ct=0.

The point x=0 and ct=0 is called the present. Coordinates in spacetime that are inside the light cone and have time coordinates greater than zero are in the future; locations inside the light cone with negative time are in the past.

                                                                       

Consider that we are located at the present. We know that, for example, we can not know what happened at the star Alpha Centauri yesterday; it is about 4 light years away and since no information can travel faster than the speed of light we will have to wait four years to find out what happened there. Thus the coordinate of Alpha Centauri yesterday, which is outside the light cone, is inaccessible to us. Similarly, we can not get a signal to Alpha Centauri that will arrive tomorrow. Thus the entire region of spacetime outside the light cone is called elsewhere.

WHY TIME RUN SLOW IN SPEED :

A reasonable question at this point is: if moving clocks run slowly,

We are going far too slowly for any noticeable change to take place.Even if we go at high enough speeds to bring about a large slowing down of local time we wouldn't notice because our own body clocks would also be running just as slowly.

The speed of light is very close to 300,000 km per second (186,300 miles per second). It isn't until we get to speeds that are a large fraction of the speed of light that any change in the flow of time becomes apparent. However, at speeds very close to that of light the effect grows in magnitude very rapidly indeed until time almost comes to a standstill.This slowing down of clocks due to high speeds is called time dilation and has a precise mathematical relationship. For the sake of completeness I have included the relevant equation below but you can skip over it and move on to the graph below it if you prefer. The equation for time dilation is:

When the equation is plotted as a graph we can easily see the dramatic effect of time dilation as the speed of light is approached:

So, when we move, at whatever speed, time slows down relative to a stationary observer. But note that, for example, the occupants of a rocket travelling at very high speeds would still experience time passing normally. However, if they could see out to an Earth-bound clock it would appear, to them, to be running too quickly. If an Earth-bound observer could see a clock inside the rocket it would appear to be running too slowly. This is why the theory is called "relativity", it is because time is relative to whoever is observing it at a particular speed.

MASS INCREASED DUE TO VELOCITY :

As our speed goes ever higher so the apparent mass increases, and so does the energy required to move it. At the speed of light it would take infinite energy to move any mass. Since it's clearly impossible to obtain infinite energy we can never quite reach the speed of light (but we can get as close as our energy supply, and technology, will allow). Note that the occupants of any rocket travelling at very high speeds will not be aware of any increase in mass, just as they wouldn't be aware in any change in the rate that time passes. It's only when they measure the mass of stationary observers that they will see that there has been a change in mass -- the astronauts will perceive that everything around them and their rocket has changed its mass while their own seems to have remained constant

Relativistic Mass Formula

Relativistic mass refers to mass of a body which change with the speed of the body as this speeds approaches close to speed of light, it increases with velocity and tends to infinity when the velocity approaches the speed of light.

Relativistic mass = rest mass / squared root [one minus (velocity / speed of light) squared]

The equation is:

mr = m0 / sqrt (1 – v2 / c2 )

Where:

mr: relativistic mass

m0: rest mass (invariant mass)

v: velocity

c: speed of light

THE EQUATION  :

In order to compensate for the apparent mass increase due to very high speeds we have to build it into our equations. We know that the mass increase can be accounted for by using the equation:

From this equation we know that mass (m) and the speed of light (c) are related in some way. What happens if we set the speed (v) to be very low? Einstein realized that if this is done we can account for the mass increase by using the term mc2 (the exact arguments and mathematics required to derive this are quite advanced, but an example is provided here). Using this term we now have an equation that takes into account both the kinetic energy and the mass increase due to motion, at least for low speeds

This equation seems to solve the problem. We can now predict the energy of a moving body and take into account the mass increase. What's more, we can rearrange the equation to show that:

This result is fine for low speeds, but what about speeds closer to the speed of light? We know that mass increases at high speeds, but according to the Newtonian part of the equation that isn't the case. Therefore, we need to replace the Newtonian part of the formula in order to make the equation correct at all speeds. How can we do this?We know that E – mc2 is approximately equal to the Newtonian kinetic energy when v is small, so we can use E – mc2 as the definition of relativistic kinetic energy:

We have now removed the Newtonian part of the equation. Note that we haven’t given a formula for relativistic kinetic energy. The reason for this will become apparent in a moment. Rearranging the result shows that:

It can now be seen that relativistic energy consists of two parts. The first part is kinetic and depends on the speed of the moving body, while the second part is due to the mass increase and does not depend on the speed of the body. However, both parts must be a form of energy, but what form? We can simplify the equation by setting the speed (i.e. the relativistic kinetic energy) of the moving body to be zero, thereby removing it from the equation:

We now have the famous equation in the form it's most often seen in, but what does it mean?We have seen that a moving body apparently increases in mass and has energy by virtue of its speed (the kinetic energy). Looking at the problem another way we can say that as the speed of a body gets lower there will be less and less kinetic energy until at rest the body will have no kinetic energy at all. So far so good, but what about the mass due to the speed of the body? Again, as the body slows down the mass will become progressively smaller but it can't reach zero. As noted near the start of the page, the lowest the mass can be is unity (1) and we can't just make the body disappear into nothing. The lowest possible mass the body can have is its "rest mass", i.e. the mass the body has when it is at rest. But the equation we have derived (E = mc2) isn't for mass, it's for energy. The energy must somehow be locked up in the mass of the body

: